Most artificial intelligence today is implemented using some form of neural network. In my last two articles, I introduced neural networks and showed you how to build a neural network in Java. The power of a neural network derives largely from its capacity for deep learning, and that capacity is built on the concept and execution of backpropagation with gradient descent. I’ll conclude this short series of articles with a quick dive into backpropagation and gradient descent in Java.
Backpropagation in machine learning
It’s been said that AI isn’t all that intelligent, that it is largely just backpropagation. So, what is this keystone of modern machine learning?
To understand backpropagation, you must first understand how a neural network works. Basically, a neural network is a directed graph of nodes called neurons. Neurons have a specific structure that takes inputs, multiplies them with weights, adds a bias value, and runs all that through an activation function. Neurons feed their output into other neurons until the output neurons are reached. The output neurons produce the output of the network. (See Styles of machine learning: Intro to neural networks for a more complete introduction.)
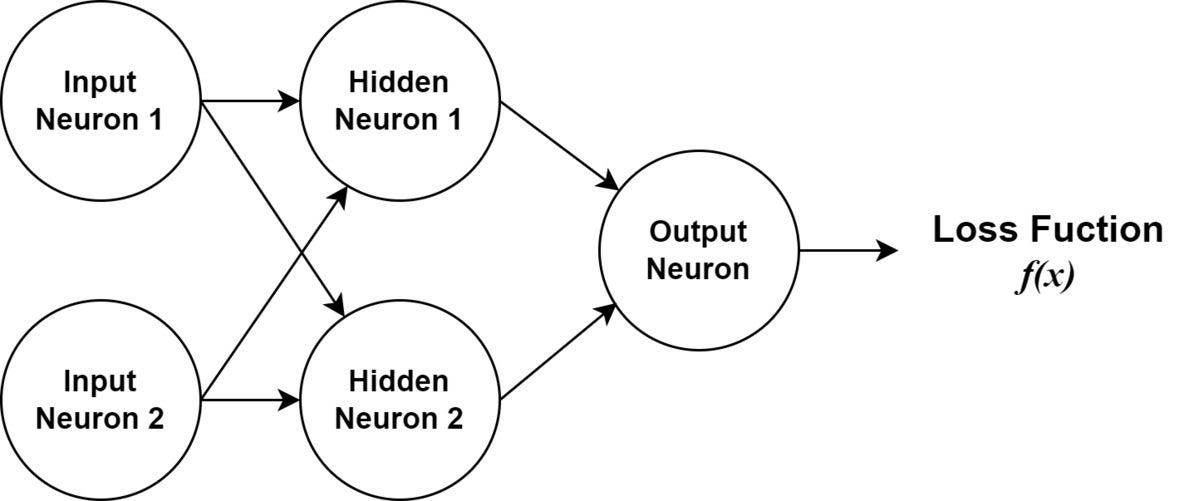
I’ll assume from here that you understand how a network and its neurons are structured, including feedforward. The example and discussion will focus on backpropagation with gradient descent. Our neural network will have a single output node, two “hidden” nodes, and two input nodes. Using a relatively simple example will make it easier to see the math involved with the algorithm. Figure 1 shows a diagram of the example neural network.
 IDG
IDGFigure 1. A diagram of the neural network we’ll use for our example.
The idea in backpropagation with gradient descent is to consider the entire network as a multivariate function that provides input to a loss function. The loss function calculates a number representing how well the network is performing by comparing the network output against known good results. The set of input data paired with good results is known as the training set. The loss function is designed to increase the number value as the network’s behavior moves further away from correct.
Gradient descent algorithms take the loss function and use partial derivatives to determine what each variable (weights and biases) in the network contributed to the loss value. It then moves backward, visiting each variable and adjusting it to decrease the loss value.
The calculus of gradient descent
Understanding gradient descent involves a few concepts from calculus. The first is the notion of a derivative. MathsIsFun.com has a great introduction to derivatives. In short, a derivative gives you the slope (or rate of change) for a function at a single point. Put another way, the derivative of a function gives us the rate of change at the given input. (The beauty of calculus is that it lets us find the change without another point of reference—or rather, it allows us to assume an infinitesimally small change to the input.)
The next important notion is the partial derivative. A partial derivative lets us take a multidimensional (also known as a multivariable) function and isolate just one of the variables to find the slope for the given dimension.
Derivatives answer the question: What is the rate of change (or slope) of a function at a specific point? Partial derivatives answer the question: Given multiple input variables to the equation, what is the rate of change for just this one variable?
Gradient descent uses these ideas to visit each variable in an equation and adjust it to minimize the output of the equation. That’s exactly what we want in training our network. If we think of the loss function as being plotted on the graph, we want to move in increments toward the minimum of a function. That is, we want to find the global minimum.
Note that the size of an increment is known as the “learning rate” in machine learning.
Gradient descent in code
We’re going to stick close to the code as we explore the mathematics of backpropagation with gradient descent. When the math gets too abstract, looking at the code will help keep us grounded. Let’s start by looking at our Neuron class, shown in Listing 1.
Listing 1. A Neuron class
class Neuron {
Random random = new Random();
private Double bias = random.nextGaussian();
private Double weight1 = random.nextGaussian();
private Double weight2 = random.nextGaussian();
public double compute(double input1, double input2){
return Util.sigmoid(this.getSum(input1, input2));
}
public Double getWeight1() { return this.weight1; }
public Double getWeight2() { return this.weight2; }
public Double getSum(double input1, double input2){ return (this.weight1 * input1) + (this.weight2 * input2) + this.bias; }
public Double getDerivedOutput(double input1, double input2){ return Util.sigmoidDeriv(this.getSum(input1, input2)); }
public void adjust(Double w1, Double w2, Double b){
this.weight1 -= w1; this.weight2 -= w2; this.bias -= b;
}
}
The Neuron class has only three Double members: weight1, weight2, and bias. It also has a few methods. The method used for feedforward is compute(). It accepts two inputs and performs the job of the neuron: multiply each by the appropriate weight, add in the bias, and run it through a sigmoid function.
Before we move on, let’s revisit the concept of the sigmoid activation, which I also discussed in my introduction to neural networks. Listing 2 shows a Java-based sigmoid activation function.
Listing 2. Util.sigmoid()
public static double sigmoid(double in){
return 1 / (1 + Math.exp(-in));
}
The sigmoid function takes the input and raises Euler’s number (Math.exp) to its negative, adding 1 and dividing that by 1. The effect is to compress the output between 0 and 1, with larger and smaller numbers approaching the limits asymptotically.
Returning to the Neuron class in Listing 1, beyond the compute() method we have getSum() and getDerivedOutput(). getSum() just does the weights * inputs + bias calculation. Notice that compute() takes getSum() and runs it through sigmoid(). The getDerivedOutput() method runs getSum() through a different function: the derivative of the sigmoid function.
Derivative in action
Now take a look at Listing 3, which shows a sigmoid derivative function in Java. We’ve talked about derivatives conceptually, here’s one in action.
Listing 3. Sigmoid derivative
public static double sigmoidDeriv(double in){
double sigmoid = Util.sigmoid(in);
return sigmoid * (1 - sigmoid);
}
Remembering that a derivative tells us what the change of a function is for a single point in its graph, we can get a feel for what this derivative is saying: Tell me the rate of change to the sigmoid function for the given input. You could say it tells us what impact the preactivated neuron from Listing 1 has on the final, activated result.
Derivative rules
You might wonder how we know the sigmoid derivative function in Listing 3 is correct. The answer is that we’ll know the derivative function is correct if it has been verified by others and if we know the properly differentiated functions are accurate based on specific rules. We don’t have to go back to first principles and rediscover these rules once we understand what they are saying and trust that they are accurate—much like we accept and apply the rules for simplifying algebraic equations.
So, in practice, we find derivatives by following the derivative rules. If you look at the sigmoid function and its derivative, you’ll see the latter can be arrived at by following these rules. For the purposes of gradient descent, we need to know about derivative rules, trust that they work, and understand how they apply. We’ll use them to find the role each of the weights and biases plays in the final loss outcome of the network.
Notation
The notation f prime f’(x) is one way of saying “the derivative of f of x”. Another is:
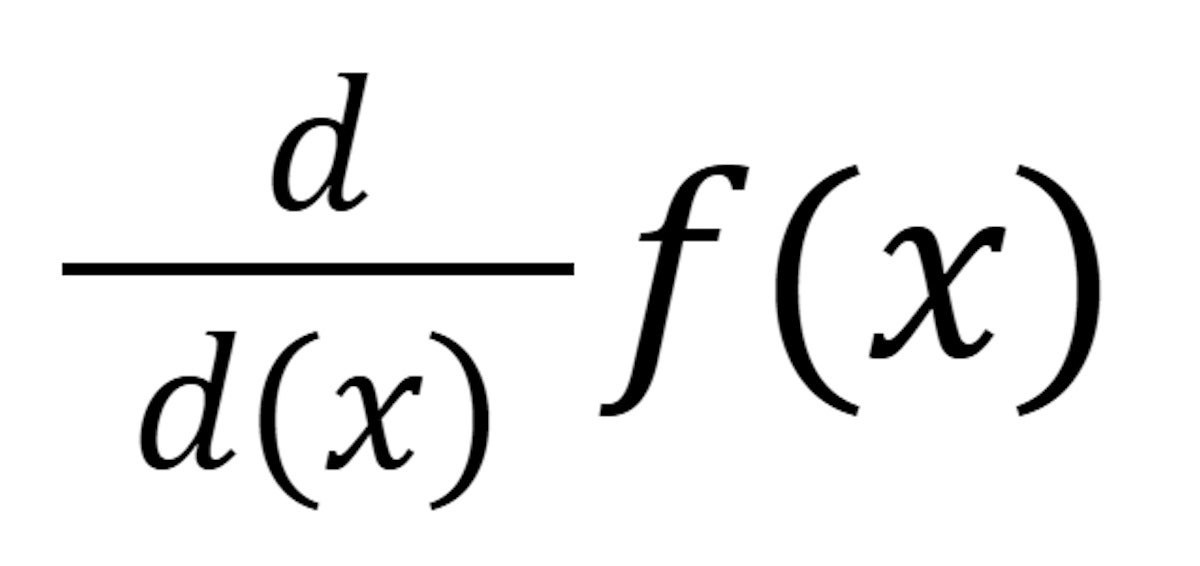 IDG
IDGThe two are equivalent:
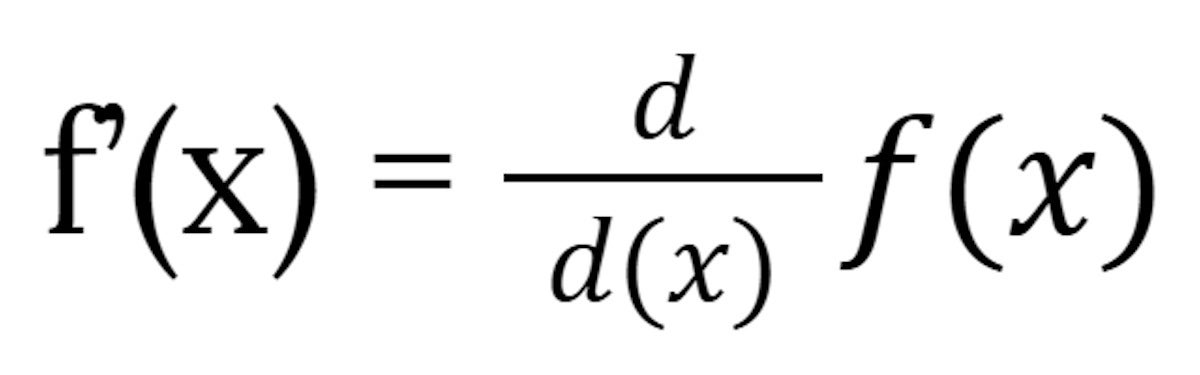 IDG
IDGAnother notation you’ll see shortly is the partial derivative notation:
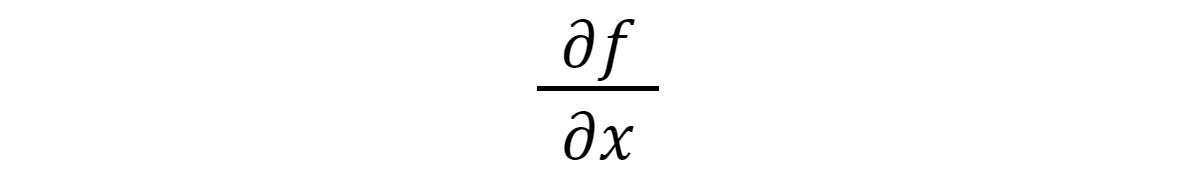 IDG
IDGThis says, give me the derivative of f for the variable x.
The chain rule
The most curious of the derivative rules is the chain rule. It says that when a function is compound (a function within a function, aka a higher-order function) you can expand it like so:
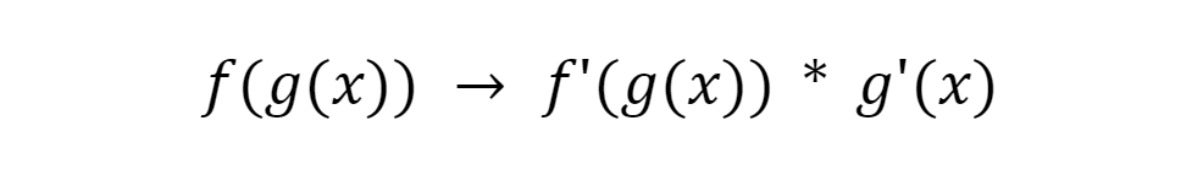 IDG
IDGWe’ll use the chain rule to unpack our network and get partial derivatives for each weight and bias.







